Computational tools¶
Statistical functions¶
Percent Change¶
Series, DataFrame, and Panel all have a method pct_change to compute the percent change over a given number of periods (using fill_method to fill NA/null values before computing the percent change).
In [1]: ser = Series(randn(8))
In [2]: ser.pct_change()
Out[2]:
0 NaN
1 -1.602976
2 4.334938
3 -0.247456
4 -2.067345
5 -1.142903
6 -1.688214
7 -9.759729
dtype: float64
In [3]: df = DataFrame(randn(10, 4))
In [4]: df.pct_change(periods=3)
Out[4]:
0 1 2 3
0 NaN NaN NaN NaN
1 NaN NaN NaN NaN
2 NaN NaN NaN NaN
3 -0.218320 -1.054001 1.987147 -0.510183
4 -0.439121 -1.816454 0.649715 -4.822809
5 -0.127833 -3.042065 -5.866604 -1.776977
6 -2.596833 -1.959538 -2.111697 -3.798900
7 -0.117826 -2.169058 0.036094 -0.067696
8 2.492606 -1.357320 -1.205802 -1.558697
9 -1.012977 2.324558 -1.003744 -0.371806
Covariance¶
The Series object has a method cov to compute covariance between series (excluding NA/null values).
In [5]: s1 = Series(randn(1000))
In [6]: s2 = Series(randn(1000))
In [7]: s1.cov(s2)
Out[7]: 0.00068010881743109993
Analogously, DataFrame has a method cov to compute pairwise covariances among the series in the DataFrame, also excluding NA/null values.
Note
Assuming the missing data are missing at random this results in an estimate for the covariance matrix which is unbiased. However, for many applications this estimate may not be acceptable because the estimated covariance matrix is not guaranteed to be positive semi-definite. This could lead to estimated correlations having absolute values which are greater than one, and/or a non-invertible covariance matrix. See Estimation of covariance matrices for more details.
In [8]: frame = DataFrame(randn(1000, 5), columns=['a', 'b', 'c', 'd', 'e'])
In [9]: frame.cov()
Out[9]:
a b c d e
a 1.000882 -0.003177 -0.002698 -0.006889 0.031912
b -0.003177 1.024721 0.000191 0.009212 0.000857
c -0.002698 0.000191 0.950735 -0.031743 -0.005087
d -0.006889 0.009212 -0.031743 1.002983 -0.047952
e 0.031912 0.000857 -0.005087 -0.047952 1.042487
DataFrame.cov also supports an optional min_periods keyword that specifies the required minimum number of observations for each column pair in order to have a valid result.
In [10]: frame = DataFrame(randn(20, 3), columns=['a', 'b', 'c'])
In [11]: frame.ix[:5, 'a'] = np.nan
In [12]: frame.ix[5:10, 'b'] = np.nan
In [13]: frame.cov()
Out[13]:
a b c
a 1.210090 -0.430629 0.018002
b -0.430629 1.240960 0.347188
c 0.018002 0.347188 1.301149
In [14]: frame.cov(min_periods=12)
Out[14]:
a b c
a 1.210090 NaN 0.018002
b NaN 1.240960 0.347188
c 0.018002 0.347188 1.301149
Correlation¶
Several methods for computing correlations are provided:
| Method name | Description |
|---|---|
| pearson (default) | Standard correlation coefficient |
| kendall | Kendall Tau correlation coefficient |
| spearman | Spearman rank correlation coefficient |
All of these are currently computed using pairwise complete observations.
Note
Please see the caveats associated with this method of calculating correlation matrices in the covariance section.
In [15]: frame = DataFrame(randn(1000, 5), columns=['a', 'b', 'c', 'd', 'e'])
In [16]: frame.ix[::2] = np.nan
# Series with Series
In [17]: frame['a'].corr(frame['b'])
Out[17]: 0.013479040400098801
In [18]: frame['a'].corr(frame['b'], method='spearman')
Out[18]: -0.0072898851595406388
# Pairwise correlation of DataFrame columns
In [19]: frame.corr()
Out[19]:
a b c d e
a 1.000000 0.013479 -0.049269 -0.042239 -0.028525
b 0.013479 1.000000 -0.020433 -0.011139 0.005654
c -0.049269 -0.020433 1.000000 0.018587 -0.054269
d -0.042239 -0.011139 0.018587 1.000000 -0.017060
e -0.028525 0.005654 -0.054269 -0.017060 1.000000
Note that non-numeric columns will be automatically excluded from the correlation calculation.
Like cov, corr also supports the optional min_periods keyword:
In [20]: frame = DataFrame(randn(20, 3), columns=['a', 'b', 'c'])
In [21]: frame.ix[:5, 'a'] = np.nan
In [22]: frame.ix[5:10, 'b'] = np.nan
In [23]: frame.corr()
Out[23]:
a b c
a 1.000000 -0.076520 0.160092
b -0.076520 1.000000 0.135967
c 0.160092 0.135967 1.000000
In [24]: frame.corr(min_periods=12)
Out[24]:
a b c
a 1.000000 NaN 0.160092
b NaN 1.000000 0.135967
c 0.160092 0.135967 1.000000
A related method corrwith is implemented on DataFrame to compute the correlation between like-labeled Series contained in different DataFrame objects.
In [25]: index = ['a', 'b', 'c', 'd', 'e']
In [26]: columns = ['one', 'two', 'three', 'four']
In [27]: df1 = DataFrame(randn(5, 4), index=index, columns=columns)
In [28]: df2 = DataFrame(randn(4, 4), index=index[:4], columns=columns)
In [29]: df1.corrwith(df2)
Out[29]:
one -0.125501
two -0.493244
three 0.344056
four 0.004183
dtype: float64
In [30]: df2.corrwith(df1, axis=1)
Out[30]:
a -0.675817
b 0.458296
c 0.190809
d -0.186275
e NaN
dtype: float64
Data ranking¶
The rank method produces a data ranking with ties being assigned the mean of the ranks (by default) for the group:
In [31]: s = Series(np.random.randn(5), index=list('abcde'))
In [32]: s['d'] = s['b'] # so there's a tie
In [33]: s.rank()
Out[33]:
a 5.0
b 2.5
c 1.0
d 2.5
e 4.0
dtype: float64
rank is also a DataFrame method and can rank either the rows (axis=0) or the columns (axis=1). NaN values are excluded from the ranking.
In [34]: df = DataFrame(np.random.randn(10, 6))
In [35]: df[4] = df[2][:5] # some ties
In [36]: df
Out[36]:
0 1 2 3 4 5
0 -0.904948 -1.163537 -1.457187 0.135463 -1.457187 0.294650
1 -0.976288 -0.244652 -0.748406 -0.999601 -0.748406 -0.800809
2 0.401965 1.460840 1.256057 1.308127 1.256057 0.876004
3 0.205954 0.369552 -0.669304 0.038378 -0.669304 1.140296
4 -0.477586 -0.730705 -1.129149 -0.601463 -1.129149 -0.211196
5 -1.092970 -0.689246 0.908114 0.204848 NaN 0.463347
6 0.376892 0.959292 0.095572 -0.593740 NaN -0.069180
7 -1.002601 1.957794 -0.120708 0.094214 NaN -1.467422
8 -0.547231 0.664402 -0.519424 -0.073254 NaN -1.263544
9 -0.250277 -0.237428 -1.056443 0.419477 NaN 1.375064
In [37]: df.rank(1)
Out[37]:
0 1 2 3 4 5
0 4 3 1.5 5 1.5 6
1 2 6 4.5 1 4.5 3
2 1 6 3.5 5 3.5 2
3 4 5 1.5 3 1.5 6
4 5 3 1.5 4 1.5 6
5 1 2 5.0 3 NaN 4
6 4 5 3.0 1 NaN 2
7 2 5 3.0 4 NaN 1
8 2 5 3.0 4 NaN 1
9 2 3 1.0 4 NaN 5
rank optionally takes a parameter ascending which by default is true; when false, data is reverse-ranked, with larger values assigned a smaller rank.
rank supports different tie-breaking methods, specified with the method parameter:
- average : average rank of tied group
- min : lowest rank in the group
- max : highest rank in the group
- first : ranks assigned in the order they appear in the array
Moving (rolling) statistics / moments¶
For working with time series data, a number of functions are provided for computing common moving or rolling statistics. Among these are count, sum, mean, median, correlation, variance, covariance, standard deviation, skewness, and kurtosis. All of these methods are in the pandas namespace, but otherwise they can be found in pandas.stats.moments.
| Function | Description |
|---|---|
| rolling_count | Number of non-null observations |
| rolling_sum | Sum of values |
| rolling_mean | Mean of values |
| rolling_median | Arithmetic median of values |
| rolling_min | Minimum |
| rolling_max | Maximum |
| rolling_std | Unbiased standard deviation |
| rolling_var | Unbiased variance |
| rolling_skew | Unbiased skewness (3rd moment) |
| rolling_kurt | Unbiased kurtosis (4th moment) |
| rolling_quantile | Sample quantile (value at %) |
| rolling_apply | Generic apply |
| rolling_cov | Unbiased covariance (binary) |
| rolling_corr | Correlation (binary) |
| rolling_window | Moving window function |
Generally these methods all have the same interface. The binary operators (e.g. rolling_corr) take two Series or DataFrames. Otherwise, they all accept the following arguments:
- window: size of moving window
- min_periods: threshold of non-null data points to require (otherwise result is NA)
- freq: optionally specify a frequency string or DateOffset to pre-conform the data to. Note that prior to pandas v0.8.0, a keyword argument time_rule was used instead of freq that referred to the legacy time rule constants
- how: optionally specify method for down or re-sampling. Default is is min for rolling_min, max for rolling_max, median for rolling_median, and mean for all other rolling functions. See DataFrame.resample()‘s how argument for more information.
These functions can be applied to ndarrays or Series objects:
In [38]: ts = Series(randn(1000), index=date_range('1/1/2000', periods=1000))
In [39]: ts = ts.cumsum()
In [40]: ts.plot(style='k--')
Out[40]: <matplotlib.axes.AxesSubplot at 0xad5fc40c>
In [41]: rolling_mean(ts, 60).plot(style='k')
Out[41]: <matplotlib.axes.AxesSubplot at 0xad5fc40c>
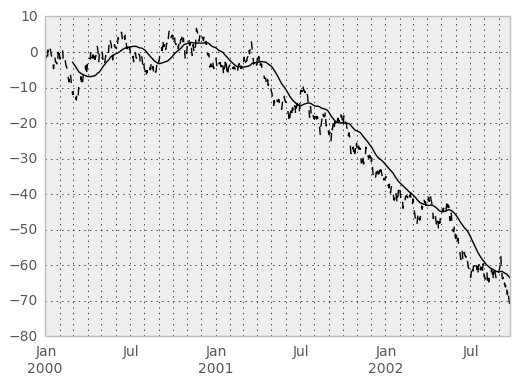
They can also be applied to DataFrame objects. This is really just syntactic sugar for applying the moving window operator to all of the DataFrame’s columns:
In [42]: df = DataFrame(randn(1000, 4), index=ts.index,
....: columns=['A', 'B', 'C', 'D'])
....:
In [43]: df = df.cumsum()
In [44]: rolling_sum(df, 60).plot(subplots=True)
Out[44]:
array([<matplotlib.axes.AxesSubplot object at 0xad3188ac>,
<matplotlib.axes.AxesSubplot object at 0xadaf56ac>,
<matplotlib.axes.AxesSubplot object at 0xadb597ec>,
<matplotlib.axes.AxesSubplot object at 0xad8a19ac>], dtype=object)
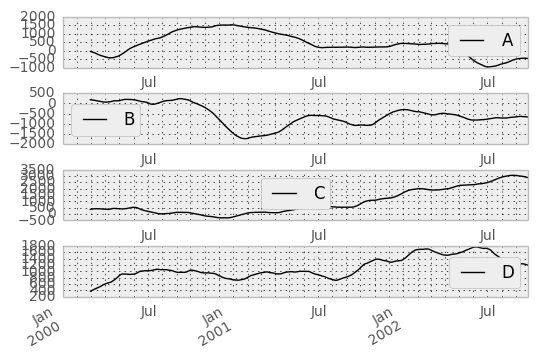
The rolling_apply function takes an extra func argument and performs generic rolling computations. The func argument should be a single function that produces a single value from an ndarray input. Suppose we wanted to compute the mean absolute deviation on a rolling basis:
In [45]: mad = lambda x: np.fabs(x - x.mean()).mean()
In [46]: rolling_apply(ts, 60, mad).plot(style='k')
Out[46]: <matplotlib.axes.AxesSubplot at 0xad5d470c>
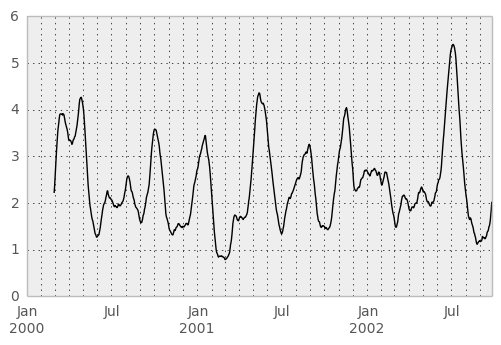
The rolling_window function performs a generic rolling window computation on the input data. The weights used in the window are specified by the win_type keyword. The list of recognized types are:
- boxcar
- triang
- blackman
- hamming
- bartlett
- parzen
- bohman
- blackmanharris
- nuttall
- barthann
- kaiser (needs beta)
- gaussian (needs std)
- general_gaussian (needs power, width)
- slepian (needs width).
In [47]: ser = Series(randn(10), index=date_range('1/1/2000', periods=10))
In [48]: rolling_window(ser, 5, 'triang')
Out[48]:
2000-01-01 NaN
2000-01-02 NaN
2000-01-03 NaN
2000-01-04 NaN
2000-01-05 -0.622722
2000-01-06 -0.460623
2000-01-07 -0.229918
2000-01-08 -0.237308
2000-01-09 -0.335064
2000-01-10 -0.403449
Freq: D, dtype: float64
Note that the boxcar window is equivalent to rolling_mean:
In [49]: rolling_window(ser, 5, 'boxcar')
Out[49]:
2000-01-01 NaN
2000-01-02 NaN
2000-01-03 NaN
2000-01-04 NaN
2000-01-05 -0.841164
2000-01-06 -0.779948
2000-01-07 -0.565487
2000-01-08 -0.502815
2000-01-09 -0.553755
2000-01-10 -0.472211
Freq: D, dtype: float64
In [50]: rolling_mean(ser, 5)
Out[50]:
2000-01-01 NaN
2000-01-02 NaN
2000-01-03 NaN
2000-01-04 NaN
2000-01-05 -0.841164
2000-01-06 -0.779948
2000-01-07 -0.565487
2000-01-08 -0.502815
2000-01-09 -0.553755
2000-01-10 -0.472211
Freq: D, dtype: float64
For some windowing functions, additional parameters must be specified:
In [51]: rolling_window(ser, 5, 'gaussian', std=0.1)
Out[51]:
2000-01-01 NaN
2000-01-02 NaN
2000-01-03 NaN
2000-01-04 NaN
2000-01-05 -0.261998
2000-01-06 -0.230600
2000-01-07 0.121276
2000-01-08 -0.136220
2000-01-09 -0.057945
2000-01-10 -0.199326
Freq: D, dtype: float64
By default the labels are set to the right edge of the window, but a center keyword is available so the labels can be set at the center. This keyword is available in other rolling functions as well.
In [52]: rolling_window(ser, 5, 'boxcar')
Out[52]:
2000-01-01 NaN
2000-01-02 NaN
2000-01-03 NaN
2000-01-04 NaN
2000-01-05 -0.841164
2000-01-06 -0.779948
2000-01-07 -0.565487
2000-01-08 -0.502815
2000-01-09 -0.553755
2000-01-10 -0.472211
Freq: D, dtype: float64
In [53]: rolling_window(ser, 5, 'boxcar', center=True)
Out[53]:
2000-01-01 NaN
2000-01-02 NaN
2000-01-03 -0.841164
2000-01-04 -0.779948
2000-01-05 -0.565487
2000-01-06 -0.502815
2000-01-07 -0.553755
2000-01-08 -0.472211
2000-01-09 NaN
2000-01-10 NaN
Freq: D, dtype: float64
In [54]: rolling_mean(ser, 5, center=True)
Out[54]:
2000-01-01 NaN
2000-01-02 NaN
2000-01-03 -0.841164
2000-01-04 -0.779948
2000-01-05 -0.565487
2000-01-06 -0.502815
2000-01-07 -0.553755
2000-01-08 -0.472211
2000-01-09 NaN
2000-01-10 NaN
Freq: D, dtype: float64
Binary rolling moments¶
rolling_cov and rolling_corr can compute moving window statistics about two Series or any combination of DataFrame/Series or DataFrame/DataFrame. Here is the behavior in each case:
- two Series: compute the statistic for the pairing.
- DataFrame/Series: compute the statistics for each column of the DataFrame with the passed Series, thus returning a DataFrame.
- DataFrame/DataFrame: by default compute the statistic for matching column names, returning a DataFrame. If the keyword argument pairwise=True is passed then computes the statistic for each pair of columns, returning a Panel whose items are the dates in question (see the next section).
For example:
In [55]: df2 = df[:20]
In [56]: rolling_corr(df2, df2['B'], window=5)
Out[56]:
A B C D
2000-01-01 NaN NaN NaN NaN
2000-01-02 NaN NaN NaN NaN
2000-01-03 NaN NaN NaN NaN
2000-01-04 NaN NaN NaN NaN
2000-01-05 -0.262853 1 0.334449 0.193380
2000-01-06 -0.083745 1 -0.521587 -0.556126
2000-01-07 -0.292940 1 -0.658532 -0.458128
... ... .. ... ...
2000-01-14 0.519499 1 -0.687277 0.192822
2000-01-15 0.048982 1 0.167669 -0.061463
2000-01-16 0.217190 1 0.167564 -0.326034
2000-01-17 0.641180 1 -0.164780 -0.111487
2000-01-18 0.130422 1 0.322833 0.632383
2000-01-19 0.317278 1 0.384528 0.813656
2000-01-20 0.293598 1 0.159538 0.742381
[20 rows x 4 columns]
Computing rolling pairwise covariances and correlations¶
In financial data analysis and other fields it’s common to compute covariance and correlation matrices for a collection of time series. Often one is also interested in moving-window covariance and correlation matrices. This can be done by passing the pairwise keyword argument, which in the case of DataFrame inputs will yield a Panel whose items are the dates in question. In the case of a single DataFrame argument the pairwise argument can even be omitted:
Note
Missing values are ignored and each entry is computed using the pairwise complete observations. Please see the covariance section for caveats associated with this method of calculating covariance and correlation matrices.
In [57]: covs = rolling_cov(df[['B','C','D']], df[['A','B','C']], 50, pairwise=True)
In [58]: covs[df.index[-50]]
Out[58]:
A B C
B 2.667506 1.671711 1.938634
C 8.513843 1.938634 10.556436
D -7.714737 -1.434529 -7.082653
In [59]: correls = rolling_corr(df, 50)
In [60]: correls[df.index[-50]]
Out[60]:
A B C D
A 1.000000 0.604221 0.767429 -0.776170
B 0.604221 1.000000 0.461484 -0.381148
C 0.767429 0.461484 1.000000 -0.748863
D -0.776170 -0.381148 -0.748863 1.000000
Note
Prior to version 0.14 this was available through rolling_corr_pairwise which is now simply syntactic sugar for calling rolling_corr(..., pairwise=True) and deprecated. This is likely to be removed in a future release.
You can efficiently retrieve the time series of correlations between two columns using ix indexing:
In [61]: correls.ix[:, 'A', 'C'].plot()
Out[61]: <matplotlib.axes.AxesSubplot at 0xad7a9bec>
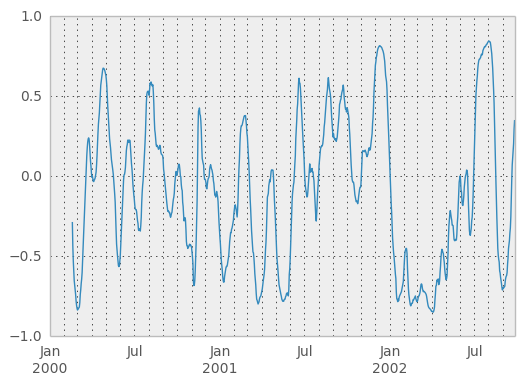
Expanding window moment functions¶
A common alternative to rolling statistics is to use an expanding window, which yields the value of the statistic with all the data available up to that point in time. As these calculations are a special case of rolling statistics, they are implemented in pandas such that the following two calls are equivalent:
In [62]: rolling_mean(df, window=len(df), min_periods=1)[:5]
Out[62]:
A B C D
2000-01-01 -1.388345 3.317290 0.344542 -0.036968
2000-01-02 -1.123132 3.622300 1.675867 0.595300
2000-01-03 -0.628502 3.626503 2.455240 1.060158
2000-01-04 -0.768740 3.888917 2.451354 1.281874
2000-01-05 -0.824034 4.108035 2.556112 1.140723
In [63]: expanding_mean(df)[:5]
Out[63]:
A B C D
2000-01-01 -1.388345 3.317290 0.344542 -0.036968
2000-01-02 -1.123132 3.622300 1.675867 0.595300
2000-01-03 -0.628502 3.626503 2.455240 1.060158
2000-01-04 -0.768740 3.888917 2.451354 1.281874
2000-01-05 -0.824034 4.108035 2.556112 1.140723
Like the rolling_ functions, the following methods are included in the pandas namespace or can be located in pandas.stats.moments.
| Function | Description |
|---|---|
| expanding_count | Number of non-null observations |
| expanding_sum | Sum of values |
| expanding_mean | Mean of values |
| expanding_median | Arithmetic median of values |
| expanding_min | Minimum |
| expanding_max | Maximum |
| expanding_std | Unbiased standard deviation |
| expanding_var | Unbiased variance |
| expanding_skew | Unbiased skewness (3rd moment) |
| expanding_kurt | Unbiased kurtosis (4th moment) |
| expanding_quantile | Sample quantile (value at %) |
| expanding_apply | Generic apply |
| expanding_cov | Unbiased covariance (binary) |
| expanding_corr | Correlation (binary) |
Aside from not having a window parameter, these functions have the same interfaces as their rolling_ counterpart. Like above, the parameters they all accept are:
- min_periods: threshold of non-null data points to require. Defaults to minimum needed to compute statistic. No NaNs will be output once min_periods non-null data points have been seen.
- freq: optionally specify a frequency string or DateOffset to pre-conform the data to. Note that prior to pandas v0.8.0, a keyword argument time_rule was used instead of freq that referred to the legacy time rule constants
Note
The output of the rolling_ and expanding_ functions do not return a NaN if there are at least min_periods non-null values in the current window. This differs from cumsum, cumprod, cummax, and cummin, which return NaN in the output wherever a NaN is encountered in the input.
An expanding window statistic will be more stable (and less responsive) than its rolling window counterpart as the increasing window size decreases the relative impact of an individual data point. As an example, here is the expanding_mean output for the previous time series dataset:
In [64]: ts.plot(style='k--')
Out[64]: <matplotlib.axes.AxesSubplot at 0xad7f446c>
In [65]: expanding_mean(ts).plot(style='k')
Out[65]: <matplotlib.axes.AxesSubplot at 0xad7f446c>
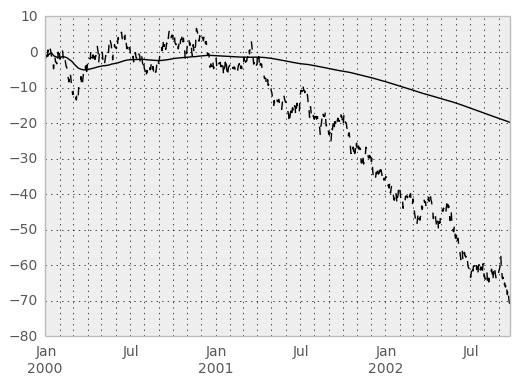
Exponentially weighted moment functions¶
A related set of functions are exponentially weighted versions of many of the
above statistics. A number of EW (exponentially weighted) functions are
provided using the blending method. For example, where 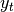 is the
result and
is the
result and 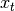 the input, we compute an exponentially weighted moving
average as
the input, we compute an exponentially weighted moving
average as
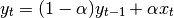
One must have 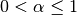 , but rather than pass
, but rather than pass 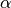 directly, it’s easier to think about either the span, center of mass
(com) or halflife of an EW moment:
directly, it’s easier to think about either the span, center of mass
(com) or halflife of an EW moment:

Note
the equation above is sometimes written in the form
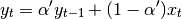
where 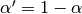 .
.
You can pass one of the three to these functions but not more. Span corresponds to what is commonly called a “20-day EW moving average” for example. Center of mass has a more physical interpretation. For example, span = 20 corresponds to com = 9.5. Halflife is the period of time for the exponential weight to reduce to one half. Here is the list of functions available:
| Function | Description |
|---|---|
| ewma | EW moving average |
| ewmvar | EW moving variance |
| ewmstd | EW moving standard deviation |
| ewmcorr | EW moving correlation |
| ewmcov | EW moving covariance |
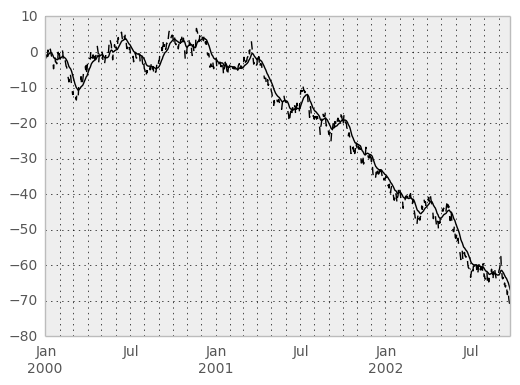
Here are an example for a univariate time series:
In [66]: plt.close('all')
In [67]: ts.plot(style='k--')
Out[67]: <matplotlib.axes.AxesSubplot at 0xad5d494c>
In [68]: ewma(ts, span=20).plot(style='k')
Out[68]: <matplotlib.axes.AxesSubplot at 0xad5d494c>
Note
The EW functions perform a standard adjustment to the initial observations whereby if there are fewer observations than called for in the span, those observations are reweighted accordingly.