pandas.stats.moments.ewmcorr

pandas.stats.moments.ewmcorr(arg1, arg2=None, com=None, span=None, halflife=None, min_periods=0, freq=None, pairwise=None, how=None, ignore_na=False, adjust=True)

Exponentially-weighted moving correlation

Parameters:

arg1 : Series, DataFrame, or ndarray

arg2 : Series, DataFrame, or ndarray, optional

if not supplied then will default to arg1 and produce pairwise output

com : float. optional

Center of mass: ,

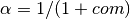span : float, optional

Specify decay in terms of span,

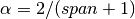
halflife : float, optional

Specify decay in terms of halflife,

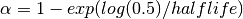
min_periods : int, default 0

Minimum number of observations in window required to have a value (otherwise result is NA).

freq : None or string alias / date offset object, default=None

Frequency to conform to before computing statistic

adjust : boolean, default True

Divide by decaying adjustment factor in beginning periods to account for imbalance in relative weightings (viewing EWMA as a moving average)

how : string, default ‘mean’

Method for down- or re-sampling

ignore_na : boolean, default False

Ignore missing values when calculating weights; specify True to reproduce pre-0.15.0 behavior

pairwise : bool, default False

If False then only matching columns between arg1 and arg2 will be used and the output will be a DataFrame. If True then all pairwise combinations will be calculated and the output will be a Panel in the case of DataFrame inputs. In the case of missing elements, only complete pairwise observations will be used.

Returns:

y : type of input argument

Notes

Either center of mass or span must be specified

EWMA is sometimes specified using a “span” parameter s, we have that the decay parameter 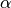is related to the span as

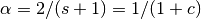
where c is the center of mass. Given a span, the associated center of mass is

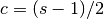
So a “20-day EWMA” would have center 9.5.

When adjust is True (default), weighted averages are calculated using weights

(1-alpha)**(n-1), (1-alpha)**(n-2), ..., 1-alpha, 1.

When adjust is False, weighted averages are calculated recursively as:

weighted_average[0] = arg[0]; weighted_average[i] = (1-alpha)*weighted_average[i-1] + alpha*arg[i].

When ignore_na is False (default), weights are based on absolute positions. For example, the weights of x and y used in calculating the final weighted average of [x, None, y] are (1-alpha)**2 and 1 (if adjust is True), and (1-alpha)**2 and alpha (if adjust is False).

When ignore_na is True (reproducing pre-0.15.0 behavior), weights are based on relative positions. For example, the weights of x and y used in calculating the final weighted average of [x, None, y] are 1-alpha and 1 (if adjust is True), and 1-alpha and alpha (if adjust is False).