Enhancing Performance¶
Cython (Writing C extensions for pandas)¶
For many use cases writing pandas in pure python and numpy is sufficient. In some computationally heavy applications however, it can be possible to achieve sizeable speed-ups by offloading work to cython.
This tutorial assumes you have refactored as much as possible in python, for example trying to remove for loops and making use of numpy vectorization, it’s always worth optimising in python first.
This tutorial walks through a “typical” process of cythonizing a slow computation. We use an example from the cython documentation but in the context of pandas. Our final cythonized solution is around 100 times faster than the pure python.
Pure python¶
We have a DataFrame to which we want to apply a function row-wise.
In [1]: df = pd.DataFrame({'a': np.random.randn(1000),
...: 'b': np.random.randn(1000),
...: 'N': np.random.randint(100, 1000, (1000)),
...: 'x': 'x'})
...:
In [2]: df
Out[2]:
N a b x
0 585 0.469112 -0.218470 x
1 841 -0.282863 -0.061645 x
2 251 -1.509059 -0.723780 x
3 972 -1.135632 0.551225 x
4 181 1.212112 -0.497767 x
5 458 -0.173215 0.837519 x
6 159 0.119209 1.103245 x
.. ... ... ... ..
993 190 0.131892 0.290162 x
994 931 0.342097 0.215341 x
995 374 -1.512743 0.874737 x
996 246 0.933753 1.120790 x
997 157 -0.308013 0.198768 x
998 977 -0.079915 1.757555 x
999 770 -1.010589 -1.115680 x
[1000 rows x 4 columns]
Here’s the function in pure python:
In [3]: def f(x):
...: return x * (x - 1)
...:
In [4]: def integrate_f(a, b, N):
...: s = 0
...: dx = (b - a) / N
...: for i in range(N):
...: s += f(a + i * dx)
...: return s * dx
...:
We achieve our result by using apply (row-wise):
In [7]: %timeit df.apply(lambda x: integrate_f(x['a'], x['b'], x['N']), axis=1)
10 loops, best of 3: 174 ms per loop
But clearly this isn’t fast enough for us. Let’s take a look and see where the time is spent during this operation (limited to the most time consuming four calls) using the prun ipython magic function:
In [5]: %prun -l 4 df.apply(lambda x: integrate_f(x['a'], x['b'], x['N']), axis=1)
629841 function calls (627827 primitive calls) in 0.601 seconds
Ordered by: internal time
List reduced from 109 to 4 due to restriction <4>
ncalls tottime percall cumtime percall filename:lineno(function)
1000 0.314 0.000 0.510 0.001 <ipython-input-4-91e33489f136>:1(integrate_f)
552423 0.186 0.000 0.186 0.000 <ipython-input-3-bc41a25943f6>:1(f)
1000 0.010 0.000 0.010 0.000 {range}
3000 0.009 0.000 0.053 0.000 index.py:1770(get_value)
By far the majority of time is spend inside either integrate_f or f, hence we’ll concentrate our efforts cythonizing these two functions.
Note
In python 2 replacing the range with its generator counterpart (xrange) would mean the range line would vanish. In python 3 range is already a generator.
Plain cython¶
First we’re going to need to import the cython magic function to ipython (for cython versions >=0.21 you can use %load_ext Cython):
In [6]: %load_ext cythonmagic
Now, let’s simply copy our functions over to cython as is (the suffix is here to distinguish between function versions):
In [7]: %%cython
...: def f_plain(x):
...: return x * (x - 1)
...: def integrate_f_plain(a, b, N):
...: s = 0
...: dx = (b - a) / N
...: for i in range(N):
...: s += f_plain(a + i * dx)
...: return s * dx
...:
Note
If you’re having trouble pasting the above into your ipython, you may need to be using bleeding edge ipython for paste to play well with cell magics.
In [4]: %timeit df.apply(lambda x: integrate_f_plain(x['a'], x['b'], x['N']), axis=1)
10 loops, best of 3: 85.5 ms per loop
Already this has shaved a third off, not too bad for a simple copy and paste.
Adding type¶
We get another huge improvement simply by providing type information:
In [8]: %%cython
...: cdef double f_typed(double x) except? -2:
...: return x * (x - 1)
...: cpdef double integrate_f_typed(double a, double b, int N):
...: cdef int i
...: cdef double s, dx
...: s = 0
...: dx = (b - a) / N
...: for i in range(N):
...: s += f_typed(a + i * dx)
...: return s * dx
...:
In [4]: %timeit df.apply(lambda x: integrate_f_typed(x['a'], x['b'], x['N']), axis=1)
10 loops, best of 3: 20.3 ms per loop
Now, we’re talking! It’s now over ten times faster than the original python implementation, and we haven’t really modified the code. Let’s have another look at what’s eating up time:
In [9]: %prun -l 4 df.apply(lambda x: integrate_f_typed(x['a'], x['b'], x['N']), axis=1)
76418 function calls (74404 primitive calls) in 0.095 seconds
Ordered by: internal time
List reduced from 107 to 4 due to restriction <4>
ncalls tottime percall cumtime percall filename:lineno(function)
3000 0.010 0.000 0.055 0.000 index.py:1770(get_value)
3000 0.007 0.000 0.068 0.000 series.py:555(__getitem__)
6000 0.007 0.000 0.025 0.000 {pandas.lib.values_from_object}
3000 0.007 0.000 0.016 0.000 internals.py:3836(get_values)
Using ndarray¶
It’s calling series... a lot! It’s creating a Series from each row, and get-ting from both the index and the series (three times for each row). Function calls are expensive in python, so maybe we could minimise these by cythonizing the apply part.
Note
We are now passing ndarrays into the cython function, fortunately cython plays very nicely with numpy.
In [10]: %%cython
....: cimport numpy as np
....: import numpy as np
....: cdef double f_typed(double x) except? -2:
....: return x * (x - 1)
....: cpdef double integrate_f_typed(double a, double b, int N):
....: cdef int i
....: cdef double s, dx
....: s = 0
....: dx = (b - a) / N
....: for i in range(N):
....: s += f_typed(a + i * dx)
....: return s * dx
....: cpdef np.ndarray[double] apply_integrate_f(np.ndarray col_a, np.ndarray col_b, np.ndarray col_N):
....: assert (col_a.dtype == np.float and col_b.dtype == np.float and col_N.dtype == np.int)
....: cdef Py_ssize_t i, n = len(col_N)
....: assert (len(col_a) == len(col_b) == n)
....: cdef np.ndarray[double] res = np.empty(n)
....: for i in range(len(col_a)):
....: res[i] = integrate_f_typed(col_a[i], col_b[i], col_N[i])
....: return res
....:
The implementation is simple, it creates an array of zeros and loops over the rows, applying our integrate_f_typed, and putting this in the zeros array.
Warning
In 0.13.0 since Series has internaly been refactored to no longer sub-class ndarray but instead subclass NDFrame, you can not pass a Series directly as a ndarray typed parameter to a cython function. Instead pass the actual ndarray using the .values attribute of the Series.
Prior to 0.13.0
apply_integrate_f(df['a'], df['b'], df['N'])
Use .values to get the underlying ndarray
apply_integrate_f(df['a'].values, df['b'].values, df['N'].values)
Note
Loops like this would be extremely slow in python, but in Cython looping over numpy arrays is fast.
In [4]: %timeit apply_integrate_f(df['a'].values, df['b'].values, df['N'].values)
1000 loops, best of 3: 1.25 ms per loop
We’ve gotten another big improvement. Let’s check again where the time is spent:
In [11]: %prun -l 4 apply_integrate_f(df['a'].values, df['b'].values, df['N'].values)
187 function calls in 0.008 seconds
Ordered by: internal time
List reduced from 48 to 4 due to restriction <4>
ncalls tottime percall cumtime percall filename:lineno(function)
1 0.006 0.006 0.006 0.006 {_cython_magic_073e22cb442403aaff864a05d833c10b.apply_integrate_f}
3 0.000 0.000 0.000 0.000 internals.py:3232(iget)
3 0.000 0.000 0.000 0.000 internals.py:3696(__init__)
6 0.000 0.000 0.000 0.000 generic.py:2362(__setattr__)
As one might expect, the majority of the time is now spent in apply_integrate_f, so if we wanted to make anymore efficiencies we must continue to concentrate our efforts here.
More advanced techniques¶
There is still hope for improvement. Here’s an example of using some more advanced cython techniques:
In [12]: %%cython
....: cimport cython
....: cimport numpy as np
....: import numpy as np
....: cdef double f_typed(double x) except? -2:
....: return x * (x - 1)
....: cpdef double integrate_f_typed(double a, double b, int N):
....: cdef int i
....: cdef double s, dx
....: s = 0
....: dx = (b - a) / N
....: for i in range(N):
....: s += f_typed(a + i * dx)
....: return s * dx
....: @cython.boundscheck(False)
....: @cython.wraparound(False)
....: cpdef np.ndarray[double] apply_integrate_f_wrap(np.ndarray[double] col_a, np.ndarray[double] col_b, np.ndarray[int] col_N):
....: cdef int i, n = len(col_N)
....: assert len(col_a) == len(col_b) == n
....: cdef np.ndarray[double] res = np.empty(n)
....: for i in range(n):
....: res[i] = integrate_f_typed(col_a[i], col_b[i], col_N[i])
....: return res
....:
In [4]: %timeit apply_integrate_f_wrap(df['a'].values, df['b'].values, df['N'].values)
1000 loops, best of 3: 987 us per loop
Even faster, with the caveat that a bug in our cython code (an off-by-one error, for example) might cause a segfault because memory access isn’t checked.
Using numba¶
A recent alternative to statically compiling cython code, is to use a dynamic jit-compiler, numba.
Numba gives you the power to speed up your applications with high performance functions written directly in Python. With a few annotations, array-oriented and math-heavy Python code can be just-in-time compiled to native machine instructions, similar in performance to C, C++ and Fortran, without having to switch languages or Python interpreters.
Numba works by generating optimized machine code using the LLVM compiler infrastructure at import time, runtime, or statically (using the included pycc tool). Numba supports compilation of Python to run on either CPU or GPU hardware, and is designed to integrate with the Python scientific software stack.
Note
You will need to install numba. This is easy with conda, by using: conda install numba, see installing using miniconda.
Note
As of numba version 0.20, pandas objects cannot be passed directly to numba-compiled functions. Instead, one must pass the numpy array underlying the pandas object to the numba-compiled function as demonstrated below.
Jit¶
Using numba to just-in-time compile your code. We simply take the plain python code from above and annotate with the @jit decorator.
import numba
@numba.jit
def f_plain(x):
return x * (x - 1)
@numba.jit
def integrate_f_numba(a, b, N):
s = 0
dx = (b - a) / N
for i in range(N):
s += f_plain(a + i * dx)
return s * dx
@numba.jit
def apply_integrate_f_numba(col_a, col_b, col_N):
n = len(col_N)
result = np.empty(n, dtype='float64')
assert len(col_a) == len(col_b) == n
for i in range(n):
result[i] = integrate_f_numba(col_a[i], col_b[i], col_N[i])
return result
def compute_numba(df):
result = apply_integrate_f_numba(df['a'].values, df['b'].values, df['N'].values)
return pd.Series(result, index=df.index, name='result')
Note that we directly pass numpy arrays to the numba function. compute_numba is just a wrapper that provides a nicer interface by passing/returning pandas objects.
In [4]: %timeit compute_numba(df)
1000 loops, best of 3: 798 us per loop
Vectorize¶
numba can also be used to write vectorized functions that do not require the user to explicitly loop over the observations of a vector; a vectorized function will be applied to each row automatically. Consider the following toy example of doubling each observation:
import numba
def double_every_value_nonumba(x):
return x*2
@numba.vectorize
def double_every_value_withnumba(x):
return x*2
# Custom function without numba
In [5]: %timeit df['col1_doubled'] = df.a.apply(double_every_value_nonumba)
1000 loops, best of 3: 797 us per loop
# Standard implementation (faster than a custom function)
In [6]: %timeit df['col1_doubled'] = df.a*2
1000 loops, best of 3: 233 us per loop
# Custom function with numba
In [7]: %timeit df['col1_doubled'] = double_every_value_withnumba(df.a.values)
1000 loops, best of 3: 145 us per loop
Caveats¶
Note
numba will execute on any function, but can only accelerate certain classes of functions.
numba is best at accelerating functions that apply numerical functions to numpy arrays. When passed a function that only uses operations it knows how to accelerate, it will execute in nopython mode.
If numba is passed a function that includes something it doesn’t know how to work with – a category that currently includes sets, lists, dictionaries, or string functions – it will revert to object mode. In object mode, numba will execute but your code will not speed up significantly. If you would prefer that numba throw an error if it cannot compile a function in a way that speeds up your code, pass numba the argument nopython=True (e.g. @numba.jit(nopython=True)). For more on troubleshooting numba modes, see the numba troubleshooting page.
Read more in the numba docs.
Expression Evaluation via eval() (Experimental)¶
New in version 0.13.
The top-level function pandas.eval() implements expression evaluation of Series and DataFrame objects.
Note
To benefit from using eval() you need to install numexpr. See the recommended dependencies section for more details.
The point of using eval() for expression evaluation rather than plain Python is two-fold: 1) large DataFrame objects are evaluated more efficiently and 2) large arithmetic and boolean expressions are evaluated all at once by the underlying engine (by default numexpr is used for evaluation).
Note
You should not use eval() for simple expressions or for expressions involving small DataFrames. In fact, eval() is many orders of magnitude slower for smaller expressions/objects than plain ol’ Python. A good rule of thumb is to only use eval() when you have a DataFrame with more than 10,000 rows.
eval() supports all arithmetic expressions supported by the engine in addition to some extensions available only in pandas.
Note
The larger the frame and the larger the expression the more speedup you will see from using eval().
Supported Syntax¶
These operations are supported by pandas.eval():
- Arithmetic operations except for the left shift (<<) and right shift (>>) operators, e.g., df + 2 * pi / s ** 4 % 42 - the_golden_ratio
- Comparison operations, including chained comparisons, e.g., 2 < df < df2
- Boolean operations, e.g., df < df2 and df3 < df4 or not df_bool
- list and tuple literals, e.g., [1, 2] or (1, 2)
- Attribute access, e.g., df.a
- Subscript expressions, e.g., df[0]
- Simple variable evaluation, e.g., pd.eval('df') (this is not very useful)
- Math functions, sin, cos, exp, log, expm1, log1p, sqrt, sinh, cosh, tanh, arcsin, arccos, arctan, arccosh, arcsinh, arctanh, abs and arctan2.
This Python syntax is not allowed:
- Expressions
- Function calls other than math functions.
- is/is not operations
- if expressions
- lambda expressions
- list/set/dict comprehensions
- Literal dict and set expressions
- yield expressions
- Generator expressions
- Boolean expressions consisting of only scalar values
- Statements
eval() Examples¶
pandas.eval() works well with expressions containing large arrays.
First let’s create a few decent-sized arrays to play with:
In [13]: nrows, ncols = 20000, 100
In [14]: df1, df2, df3, df4 = [pd.DataFrame(np.random.randn(nrows, ncols)) for _ in range(4)]
Now let’s compare adding them together using plain ol’ Python versus eval():
In [15]: %timeit df1 + df2 + df3 + df4
10 loops, best of 3: 24.6 ms per loop
In [16]: %timeit pd.eval('df1 + df2 + df3 + df4')
100 loops, best of 3: 14.9 ms per loop
Now let’s do the same thing but with comparisons:
In [17]: %timeit (df1 > 0) & (df2 > 0) & (df3 > 0) & (df4 > 0)
10 loops, best of 3: 72.6 ms per loop
In [18]: %timeit pd.eval('(df1 > 0) & (df2 > 0) & (df3 > 0) & (df4 > 0)')
10 loops, best of 3: 26.2 ms per loop
eval() also works with unaligned pandas objects:
In [19]: s = pd.Series(np.random.randn(50))
In [20]: %timeit df1 + df2 + df3 + df4 + s
10 loops, best of 3: 82.1 ms per loop
In [21]: %timeit pd.eval('df1 + df2 + df3 + df4 + s')
10 loops, best of 3: 58.2 ms per loop
Note
Operations such as
1 and 2 # would parse to 1 & 2, but should evaluate to 2 3 or 4 # would parse to 3 | 4, but should evaluate to 3 ~1 # this is okay, but slower when using eval
should be performed in Python. An exception will be raised if you try to perform any boolean/bitwise operations with scalar operands that are not of type bool or np.bool_. Again, you should perform these kinds of operations in plain Python.
The DataFrame.eval method (Experimental)¶
New in version 0.13.
In addition to the top level pandas.eval() function you can also evaluate an expression in the “context” of a DataFrame.
In [22]: df = pd.DataFrame(np.random.randn(5, 2), columns=['a', 'b'])
In [23]: df.eval('a + b')
Out[23]:
0 -0.246747
1 0.867786
2 -1.626063
3 -1.134978
4 -1.027798
dtype: float64
Any expression that is a valid pandas.eval() expression is also a valid DataFrame.eval() expression, with the added benefit that you don’t have to prefix the name of the DataFrame to the column(s) you’re interested in evaluating.
In addition, you can perform assignment of columns within an expression. This allows for formulaic evaluation. Only a single assignment is permitted. The assignment target can be a new column name or an existing column name, and it must be a valid Python identifier.
In [24]: df = pd.DataFrame(dict(a=range(5), b=range(5, 10)))
In [25]: df.eval('c = a + b')
In [26]: df.eval('d = a + b + c')
In [27]: df.eval('a = 1')
In [28]: df
Out[28]:
a b c d
0 1 5 5 10
1 1 6 7 14
2 1 7 9 18
3 1 8 11 22
4 1 9 13 26
The equivalent in standard Python would be
In [29]: df = pd.DataFrame(dict(a=range(5), b=range(5, 10)))
In [30]: df['c'] = df.a + df.b
In [31]: df['d'] = df.a + df.b + df.c
In [32]: df['a'] = 1
In [33]: df
Out[33]:
a b c d
0 1 5 5 10
1 1 6 7 14
2 1 7 9 18
3 1 8 11 22
4 1 9 13 26
Local Variables¶
In pandas version 0.14 the local variable API has changed. In pandas 0.13.x, you could refer to local variables the same way you would in standard Python. For example,
df = pd.DataFrame(np.random.randn(5, 2), columns=['a', 'b'])
newcol = np.random.randn(len(df))
df.eval('b + newcol')
UndefinedVariableError: name 'newcol' is not defined
As you can see from the exception generated, this syntax is no longer allowed. You must explicitly reference any local variable that you want to use in an expression by placing the @ character in front of the name. For example,
In [34]: df = pd.DataFrame(np.random.randn(5, 2), columns=list('ab'))
In [35]: newcol = np.random.randn(len(df))
In [36]: df.eval('b + @newcol')
Out[36]:
0 -0.173926
1 2.493083
2 -0.881831
3 -0.691045
4 1.334703
dtype: float64
In [37]: df.query('b < @newcol')
Out[37]:
a b
0 0.863987 -0.115998
2 -2.621419 -1.297879
If you don’t prefix the local variable with @, pandas will raise an exception telling you the variable is undefined.
When using DataFrame.eval() and DataFrame.query(), this allows you to have a local variable and a DataFrame column with the same name in an expression.
In [38]: a = np.random.randn()
In [39]: df.query('@a < a')
Out[39]:
a b
0 0.863987 -0.115998
In [40]: df.loc[a < df.a] # same as the previous expression
Out[40]:
a b
0 0.863987 -0.115998
With pandas.eval() you cannot use the @ prefix at all, because it isn’t defined in that context. pandas will let you know this if you try to use @ in a top-level call to pandas.eval(). For example,
In [41]: a, b = 1, 2
In [42]: pd.eval('@a + b')
File "<string>", line unknown
SyntaxError: The '@' prefix is not allowed in top-level eval calls,
please refer to your variables by name without the '@' prefix
In this case, you should simply refer to the variables like you would in standard Python.
In [43]: pd.eval('a + b')
Out[43]: 3
pandas.eval() Parsers¶
There are two different parsers and two different engines you can use as the backend.
The default 'pandas' parser allows a more intuitive syntax for expressing query-like operations (comparisons, conjunctions and disjunctions). In particular, the precedence of the & and | operators is made equal to the precedence of the corresponding boolean operations and and or.
For example, the above conjunction can be written without parentheses. Alternatively, you can use the 'python' parser to enforce strict Python semantics.
In [44]: expr = '(df1 > 0) & (df2 > 0) & (df3 > 0) & (df4 > 0)'
In [45]: x = pd.eval(expr, parser='python')
In [46]: expr_no_parens = 'df1 > 0 & df2 > 0 & df3 > 0 & df4 > 0'
In [47]: y = pd.eval(expr_no_parens, parser='pandas')
In [48]: np.all(x == y)
Out[48]: True
The same expression can be “anded” together with the word and as well:
In [49]: expr = '(df1 > 0) & (df2 > 0) & (df3 > 0) & (df4 > 0)'
In [50]: x = pd.eval(expr, parser='python')
In [51]: expr_with_ands = 'df1 > 0 and df2 > 0 and df3 > 0 and df4 > 0'
In [52]: y = pd.eval(expr_with_ands, parser='pandas')
In [53]: np.all(x == y)
Out[53]: True
The and and or operators here have the same precedence that they would in vanilla Python.
pandas.eval() Backends¶
There’s also the option to make eval() operate identical to plain ol’ Python.
Note
Using the 'python' engine is generally not useful, except for testing other evaluation engines against it. You will achieve no performance benefits using eval() with engine='python' and in fact may incur a performance hit.
You can see this by using pandas.eval() with the 'python' engine. It is a bit slower (not by much) than evaluating the same expression in Python
In [54]: %timeit df1 + df2 + df3 + df4
10 loops, best of 3: 24.3 ms per loop
In [55]: %timeit pd.eval('df1 + df2 + df3 + df4', engine='python')
10 loops, best of 3: 26.5 ms per loop
pandas.eval() Performance¶
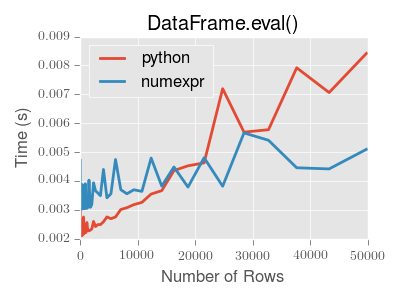
eval() is intended to speed up certain kinds of operations. In particular, those operations involving complex expressions with large DataFrame/Series objects should see a significant performance benefit. Here is a plot showing the running time of pandas.eval() as function of the size of the frame involved in the computation. The two lines are two different engines.
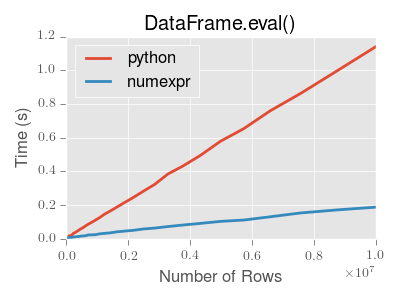
Note
Operations with smallish objects (around 15k-20k rows) are faster using plain Python:
This plot was created using a DataFrame with 3 columns each containing floating point values generated using numpy.random.randn().
Technical Minutia Regarding Expression Evaluation¶
Expressions that would result in an object dtype or involve datetime operations (because of NaT) must be evaluated in Python space. The main reason for this behavior is to maintain backwards compatbility with versions of numpy < 1.7. In those versions of numpy a call to ndarray.astype(str) will truncate any strings that are more than 60 characters in length. Second, we can’t pass object arrays to numexpr thus string comparisons must be evaluated in Python space.
The upshot is that this only applies to object-dtype’d expressions. So, if you have an expression–for example
In [56]: df = pd.DataFrame({'strings': np.repeat(list('cba'), 3),
....: 'nums': np.repeat(range(3), 3)})
....:
In [57]: df
Out[57]:
nums strings
0 0 c
1 0 c
2 0 c
3 1 b
4 1 b
5 1 b
6 2 a
7 2 a
8 2 a
In [58]: df.query('strings == "a" and nums == 1')
Out[58]:
Empty DataFrame
Columns: [nums, strings]
Index: []
the numeric part of the comparison (nums == 1) will be evaluated by numexpr.
In general, DataFrame.query()/pandas.eval() will evaluate the subexpressions that can be evaluated by numexpr and those that must be evaluated in Python space transparently to the user. This is done by inferring the result type of an expression from its arguments and operators.