pandas.DataFrame.plot.kde

DataFrame.plot.kde(bw_method=None, ind=None, **kwds)

Generate Kernel Density Estimate plot using Gaussian kernels.

In statistics, kernel density estimation (KDE) is a non-parametric way to estimate the probability density function (PDF) of a random variable. This function uses Gaussian kernels and includes automatic bandwidth determination.

Parameters:

bw_method : str, scalar or callable, optional

The method used to calculate the estimator bandwidth. This can be ‘scott’, ‘silverman’, a scalar constant or a callable. If None (default), ‘scott’ is used. See scipy.stats.gaussian_kde for more information.

ind : NumPy array or integer, optional

Evaluation points for the estimated PDF. If None (default), 1000 equally spaced points are used. If ind is a NumPy array, the KDE is evaluated at the points passed. If ind is an integer, ind number of equally spaced points are used.

**kwds : optional

Additional keyword arguments are documented in pandas.DataFrame.plot().

Returns:

axes : matplotlib.axes.Axes or numpy.ndarray of them

See also

scipy.stats.gaussian_kde

Representation of a kernel-density estimate using Gaussian kernels. This is the function used internally to estimate the PDF.

Series.plot.kde

Generate a KDE plot for a Series.

Examples

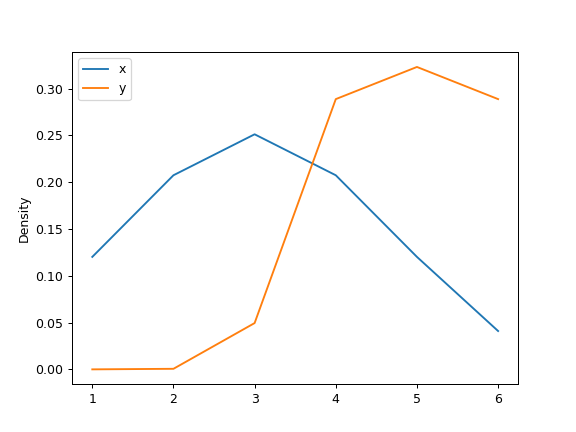
Given several Series of points randomly sampled from unknown distributions, estimate their PDFs using KDE with automatic bandwidth determination and plot the results, evaluating them at 1000 equally spaced points (default):

>>> df = pd.DataFrame({
...     'x': [1, 2, 2.5, 3, 3.5, 4, 5],
...     'y': [4, 4, 4.5, 5, 5.5, 6, 6],
... })
>>> ax = df.plot.kde()

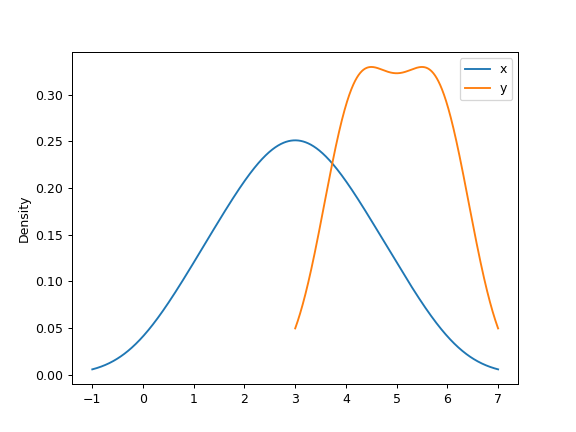
A scalar bandwidth can be specified. Using a small bandwidth value can lead to over-fitting, while using a large bandwidth value may result in under-fitting:

>>> ax = df.plot.kde(bw_method=0.3)

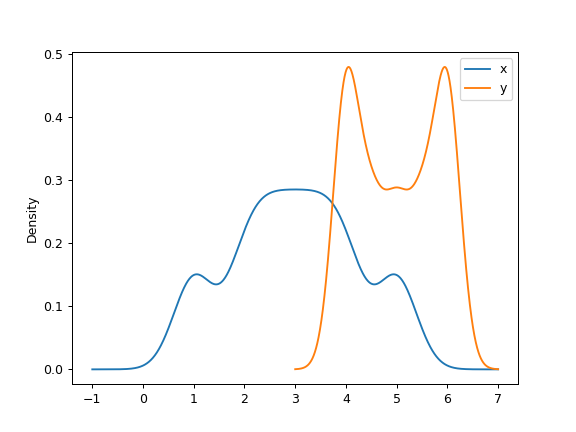
>>> ax = df.plot.kde(bw_method=3)

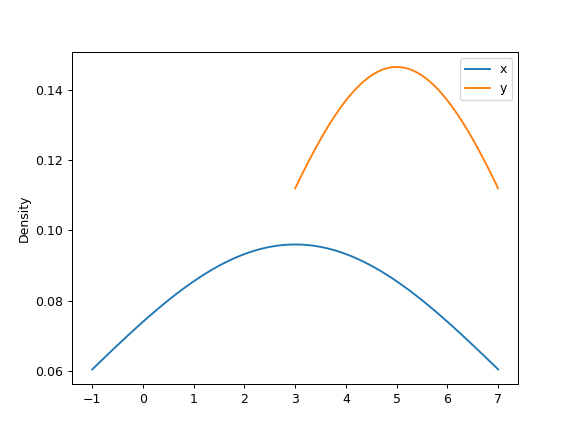
Finally, the ind parameter determines the evaluation points for the plot of the estimated PDF:

>>> ax = df.plot.kde(ind=[1, 2, 3, 4, 5, 6])