Enhancing performance#

In this part of the tutorial, we will investigate how to speed up certain functions operating on pandas DataFrame using Cython, Numba and pandas.eval(). Generally, using Cython and Numba can offer a larger speedup than using pandas.eval() but will require a lot more code.

Note

In addition to following the steps in this tutorial, users interested in enhancing performance are highly encouraged to install the recommended dependencies for pandas. These dependencies are often not installed by default, but will offer speed improvements if present.

Cython (writing C extensions for pandas)#

For many use cases writing pandas in pure Python and NumPy is sufficient. In some computationally heavy applications however, it can be possible to achieve sizable speed-ups by offloading work to cython.

This tutorial assumes you have refactored as much as possible in Python, for example by trying to remove for-loops and making use of NumPy vectorization. It’s always worth optimising in Python first.

This tutorial walks through a “typical” process of cythonizing a slow computation. We use an example from the Cython documentation but in the context of pandas. Our final cythonized solution is around 100 times faster than the pure Python solution.

Pure Python#

We have a DataFrame to which we want to apply a function row-wise.

In [1]: df = pd.DataFrame(
   ...:     {
   ...:         "a": np.random.randn(1000),
   ...:         "b": np.random.randn(1000),
   ...:         "N": np.random.randint(100, 1000, (1000)),
   ...:         "x": "x",
   ...:     }
   ...: )
   ...: 

In [2]: df
Out[2]: 
            a         b    N  x
0    0.469112 -0.218470  585  x
1   -0.282863 -0.061645  841  x
2   -1.509059 -0.723780  251  x
3   -1.135632  0.551225  972  x
4    1.212112 -0.497767  181  x
..        ...       ...  ... ..
995 -1.512743  0.874737  374  x
996  0.933753  1.120790  246  x
997 -0.308013  0.198768  157  x
998 -0.079915  1.757555  977  x
999 -1.010589 -1.115680  770  x

[1000 rows x 4 columns]

Here’s the function in pure Python:

In [3]: def f(x):
   ...:     return x * (x - 1)
   ...: 

In [4]: def integrate_f(a, b, N):
   ...:     s = 0
   ...:     dx = (b - a) / N
   ...:     for i in range(N):
   ...:         s += f(a + i * dx)
   ...:     return s * dx
   ...: 

We achieve our result by using DataFrame.apply() (row-wise):

In [5]: %timeit df.apply(lambda x: integrate_f(x["a"], x["b"], x["N"]), axis=1)
76.8 ms +- 481 us per loop (mean +- std. dev. of 7 runs, 10 loops each)

Let’s take a look and see where the time is spent during this operation using the prun ipython magic function:

# most time consuming 4 calls
In [6]: %prun -l 4 df.apply(lambda x: integrate_f(x["a"], x["b"], x["N"]), axis=1)  # noqa E999
         617986 function calls (617968 primitive calls) in 0.172 seconds

   Ordered by: internal time
   List reduced from 177 to 4 due to restriction <4>

   ncalls  tottime  percall  cumtime  percall filename:lineno(function)
     1000    0.099    0.000    0.151    0.000 <ipython-input-4-c2a74e076cf0>:1(integrate_f)
   552423    0.052    0.000    0.052    0.000 <ipython-input-3-c138bdd570e3>:1(f)
     3000    0.004    0.000    0.015    0.000 series.py:1016(__getitem__)
     3000    0.003    0.000    0.007    0.000 series.py:1139(_get_value)

By far the majority of time is spend inside either integrate_f or f, hence we’ll concentrate our efforts cythonizing these two functions.

Plain Cython#

First we’re going to need to import the Cython magic function to IPython:

In [7]: %load_ext Cython

Now, let’s simply copy our functions over to Cython:

In [8]: %%cython
   ...: def f_plain(x):
   ...:     return x * (x - 1)
   ...: def integrate_f_plain(a, b, N):
   ...:     s = 0
   ...:     dx = (b - a) / N
   ...:     for i in range(N):
   ...:         s += f_plain(a + i * dx)
   ...:     return s * dx
   ...: 

In [9]: %timeit df.apply(lambda x: integrate_f_plain(x["a"], x["b"], x["N"]), axis=1)
46 ms +- 364 us per loop (mean +- std. dev. of 7 runs, 10 loops each)

This has improved the performance compared to the pure Python approach by one-third.

Declaring C types#

We can annotate the function variables and return types as well as use cdef and cpdef to improve performance:

In [10]: %%cython
   ....: cdef double f_typed(double x) except? -2:
   ....:     return x * (x - 1)
   ....: cpdef double integrate_f_typed(double a, double b, int N):
   ....:     cdef int i
   ....:     cdef double s, dx
   ....:     s = 0
   ....:     dx = (b - a) / N
   ....:     for i in range(N):
   ....:         s += f_typed(a + i * dx)
   ....:     return s * dx
   ....: 

In [11]: %timeit df.apply(lambda x: integrate_f_typed(x["a"], x["b"], x["N"]), axis=1)
7.52 ms +- 56.8 us per loop (mean +- std. dev. of 7 runs, 100 loops each)

Annotating the functions with C types yields an over ten times performance improvement compared to the original Python implementation.

Using ndarray#

When re-profiling, time is spent creating a Series from each row, and calling __getitem__ from both the index and the series (three times for each row). These Python function calls are expensive and can be improved by passing an np.ndarray.

In [12]: %prun -l 4 df.apply(lambda x: integrate_f_typed(x["a"], x["b"], x["N"]), axis=1)
         65563 function calls (65545 primitive calls) in 0.024 seconds

   Ordered by: internal time
   List reduced from 176 to 4 due to restriction <4>

   ncalls  tottime  percall  cumtime  percall filename:lineno(function)
     3000    0.004    0.000    0.017    0.000 series.py:1016(__getitem__)
     3000    0.003    0.000    0.008    0.000 series.py:1139(_get_value)
     3000    0.002    0.000    0.003    0.000 indexing.py:2678(check_dict_or_set_indexers)
     3000    0.002    0.000    0.003    0.000 base.py:3763(get_loc)

In [13]: %%cython
   ....: cimport numpy as np
   ....: import numpy as np
   ....: cdef double f_typed(double x) except? -2:
   ....:     return x * (x - 1)
   ....: cpdef double integrate_f_typed(double a, double b, int N):
   ....:     cdef int i
   ....:     cdef double s, dx
   ....:     s = 0
   ....:     dx = (b - a) / N
   ....:     for i in range(N):
   ....:         s += f_typed(a + i * dx)
   ....:     return s * dx
   ....: cpdef np.ndarray[double] apply_integrate_f(np.ndarray col_a, np.ndarray col_b,
   ....:                                            np.ndarray col_N):
   ....:     assert (col_a.dtype == np.float64
   ....:             and col_b.dtype == np.float64 and col_N.dtype == np.dtype(int))
   ....:     cdef Py_ssize_t i, n = len(col_N)
   ....:     assert (len(col_a) == len(col_b) == n)
   ....:     cdef np.ndarray[double] res = np.empty(n)
   ....:     for i in range(len(col_a)):
   ....:         res[i] = integrate_f_typed(col_a[i], col_b[i], col_N[i])
   ....:     return res
   ....: 

This implementation creates an array of zeros and inserts the result of integrate_f_typed applied over each row. Looping over an ndarray is faster in Cython than looping over a Series object.

Since apply_integrate_f is typed to accept an np.ndarray, Series.to_numpy() calls are needed to utilize this function.

In [14]: %timeit apply_integrate_f(df["a"].to_numpy(), df["b"].to_numpy(), df["N"].to_numpy())
734 us +- 2.21 us per loop (mean +- std. dev. of 7 runs, 1,000 loops each)

Performance has improved from the prior implementation by almost ten times.

Disabling compiler directives#

The majority of the time is now spent in apply_integrate_f. Disabling Cython’s boundscheck and wraparound checks can yield more performance.

In [15]: %prun -l 4 apply_integrate_f(df["a"].to_numpy(), df["b"].to_numpy(), df["N"].to_numpy())
         82 function calls in 0.001 seconds

   Ordered by: internal time
   List reduced from 23 to 4 due to restriction <4>

   ncalls  tottime  percall  cumtime  percall filename:lineno(function)
        1    0.001    0.001    0.001    0.001 {built-in method _cython_magic_033574a121aaa9ad9d8ac19d6a0978d5.apply_integrate_f}
        1    0.000    0.000    0.001    0.001 {built-in method builtins.exec}
        3    0.000    0.000    0.000    0.000 frame.py:3853(__getitem__)
        3    0.000    0.000    0.000    0.000 base.py:541(to_numpy)

In [16]: %%cython
   ....: cimport cython
   ....: cimport numpy as np
   ....: import numpy as np
   ....: cdef np.float64_t f_typed(np.float64_t x) except? -2:
   ....:     return x * (x - 1)
   ....: cpdef np.float64_t integrate_f_typed(np.float64_t a, np.float64_t b, np.int64_t N):
   ....:     cdef np.int64_t i
   ....:     cdef np.float64_t s = 0.0, dx
   ....:     dx = (b - a) / N
   ....:     for i in range(N):
   ....:         s += f_typed(a + i * dx)
   ....:     return s * dx
   ....: @cython.boundscheck(False)
   ....: @cython.wraparound(False)
   ....: cpdef np.ndarray[np.float64_t] apply_integrate_f_wrap(
   ....:     np.ndarray[np.float64_t] col_a,
   ....:     np.ndarray[np.float64_t] col_b,
   ....:     np.ndarray[np.int64_t] col_N
   ....: ):
   ....:     cdef np.int64_t i, n = len(col_N)
   ....:     assert len(col_a) == len(col_b) == n
   ....:     cdef np.ndarray[np.float64_t] res = np.empty(n, dtype=np.float64)
   ....:     for i in range(n):
   ....:         res[i] = integrate_f_typed(col_a[i], col_b[i], col_N[i])
   ....:     return res
   ....: 

In [17]: %timeit apply_integrate_f_wrap(df["a"].to_numpy(), df["b"].to_numpy(), df["N"].to_numpy())
619 us +- 2.68 us per loop (mean +- std. dev. of 7 runs, 1,000 loops each)

However, a loop indexer i accessing an invalid location in an array would cause a segfault because memory access isn’t checked. For more about boundscheck and wraparound, see the Cython docs on compiler directives.

Numba (JIT compilation)#

An alternative to statically compiling Cython code is to use a dynamic just-in-time (JIT) compiler with Numba.

Numba allows you to write a pure Python function which can be JIT compiled to native machine instructions, similar in performance to C, C++ and Fortran, by decorating your function with @jit.

Numba works by generating optimized machine code using the LLVM compiler infrastructure at import time, runtime, or statically (using the included pycc tool). Numba supports compilation of Python to run on either CPU or GPU hardware and is designed to integrate with the Python scientific software stack.

Note

The @jit compilation will add overhead to the runtime of the function, so performance benefits may not be realized especially when using small data sets. Consider caching your function to avoid compilation overhead each time your function is run.

Numba can be used in 2 ways with pandas:

Specify the engine="numba" keyword in select pandas methods
Define your own Python function decorated with @jit and pass the underlying NumPy array of Series or DataFrame (using Series.to_numpy()) into the function

pandas Numba Engine#

If Numba is installed, one can specify engine="numba" in select pandas methods to execute the method using Numba. Methods that support engine="numba" will also have an engine_kwargs keyword that accepts a dictionary that allows one to specify "nogil", "nopython" and "parallel" keys with boolean values to pass into the @jit decorator. If engine_kwargs is not specified, it defaults to {"nogil": False, "nopython": True, "parallel": False} unless otherwise specified.

Note

In terms of performance, the first time a function is run using the Numba engine will be slow as Numba will have some function compilation overhead. However, the JIT compiled functions are cached, and subsequent calls will be fast. In general, the Numba engine is performant with a larger amount of data points (e.g. 1+ million).

In [1]: data = pd.Series(range(1_000_000))  # noqa: E225

In [2]: roll = data.rolling(10)

In [3]: def f(x):
   ...:     return np.sum(x) + 5
# Run the first time, compilation time will affect performance
In [4]: %timeit -r 1 -n 1 roll.apply(f, engine='numba', raw=True)
1.23 s ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
# Function is cached and performance will improve
In [5]: %timeit roll.apply(f, engine='numba', raw=True)
188 ms ± 1.93 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

In [6]: %timeit roll.apply(f, engine='cython', raw=True)
3.92 s ± 59 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

If your compute hardware contains multiple CPUs, the largest performance gain can be realized by setting parallel to True to leverage more than 1 CPU. Internally, pandas leverages numba to parallelize computations over the columns of a DataFrame; therefore, this performance benefit is only beneficial for a DataFrame with a large number of columns.

In [1]: import numba

In [2]: numba.set_num_threads(1)

In [3]: df = pd.DataFrame(np.random.randn(10_000, 100))

In [4]: roll = df.rolling(100)

In [5]: %timeit roll.mean(engine="numba", engine_kwargs={"parallel": True})
347 ms ± 26 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

In [6]: numba.set_num_threads(2)

In [7]: %timeit roll.mean(engine="numba", engine_kwargs={"parallel": True})
201 ms ± 2.97 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

Custom Function Examples#

A custom Python function decorated with @jit can be used with pandas objects by passing their NumPy array representations with Series.to_numpy().

import numba


@numba.jit
def f_plain(x):
    return x * (x - 1)


@numba.jit
def integrate_f_numba(a, b, N):
    s = 0
    dx = (b - a) / N
    for i in range(N):
        s += f_plain(a + i * dx)
    return s * dx


@numba.jit
def apply_integrate_f_numba(col_a, col_b, col_N):
    n = len(col_N)
    result = np.empty(n, dtype="float64")
    assert len(col_a) == len(col_b) == n
    for i in range(n):
        result[i] = integrate_f_numba(col_a[i], col_b[i], col_N[i])
    return result


def compute_numba(df):
    result = apply_integrate_f_numba(
        df["a"].to_numpy(), df["b"].to_numpy(), df["N"].to_numpy()
    )
    return pd.Series(result, index=df.index, name="result")

In [4]: %timeit compute_numba(df)
1000 loops, best of 3: 798 us per loop

In this example, using Numba was faster than Cython.

Numba can also be used to write vectorized functions that do not require the user to explicitly loop over the observations of a vector; a vectorized function will be applied to each row automatically. Consider the following example of doubling each observation:

import numba


def double_every_value_nonumba(x):
    return x * 2


@numba.vectorize
def double_every_value_withnumba(x):  # noqa E501
    return x * 2

# Custom function without numba
In [5]: %timeit df["col1_doubled"] = df["a"].apply(double_every_value_nonumba)  # noqa E501
1000 loops, best of 3: 797 us per loop

# Standard implementation (faster than a custom function)
In [6]: %timeit df["col1_doubled"] = df["a"] * 2
1000 loops, best of 3: 233 us per loop

# Custom function with numba
In [7]: %timeit df["col1_doubled"] = double_every_value_withnumba(df["a"].to_numpy())
1000 loops, best of 3: 145 us per loop

Caveats#

Numba is best at accelerating functions that apply numerical functions to NumPy arrays. If you try to @jit a function that contains unsupported Python or NumPy code, compilation will revert object mode which will mostly likely not speed up your function. If you would prefer that Numba throw an error if it cannot compile a function in a way that speeds up your code, pass Numba the argument nopython=True (e.g. @jit(nopython=True)). For more on troubleshooting Numba modes, see the Numba troubleshooting page.

Using parallel=True (e.g. @jit(parallel=True)) may result in a SIGABRT if the threading layer leads to unsafe behavior. You can first specify a safe threading layer before running a JIT function with parallel=True.

Generally if the you encounter a segfault (SIGSEGV) while using Numba, please report the issue to the Numba issue tracker.

Expression evaluation via `eval()`#

The top-level function pandas.eval() implements performant expression evaluation of Series and DataFrame. Expression evaluation allows operations to be expressed as strings and can potentially provide a performance improvement by evaluate arithmetic and boolean expression all at once for large DataFrame.

Note

You should not use eval() for simple expressions or for expressions involving small DataFrames. In fact, eval() is many orders of magnitude slower for smaller expressions or objects than plain Python. A good rule of thumb is to only use eval() when you have a DataFrame with more than 10,000 rows.

Supported syntax#

These operations are supported by pandas.eval():

Arithmetic operations except for the left shift (<<) and right shift (>>) operators, e.g., df + 2 * pi / s ** 4 % 42 - the_golden_ratio
Comparison operations, including chained comparisons, e.g., 2 < df < df2
Boolean operations, e.g., df < df2 and df3 < df4 or not df_bool
list and tuple literals, e.g., [1, 2] or (1, 2)
Attribute access, e.g., df.a
Subscript expressions, e.g., df[0]
Simple variable evaluation, e.g., pd.eval("df") (this is not very useful)
Math functions: sin, cos, exp, log, expm1, log1p, sqrt, sinh, cosh, tanh, arcsin, arccos, arctan, arccosh, arcsinh, arctanh, abs, arctan2 and log10.

The following Python syntax is not allowed:

Expressions
- Function calls other than math functions.
- is/is not operations
- if expressions
- lambda expressions
- list/set/dict comprehensions
- Literal dict and set expressions
- yield expressions
- Generator expressions
- Boolean expressions consisting of only scalar values
Statements
- Neither simple or compound statements are allowed. This includes for, while, and if.

Local variables#

You must explicitly reference any local variable that you want to use in an expression by placing the @ character in front of the name. This mechanism is the same for both DataFrame.query() and DataFrame.eval(). For example,

In [18]: df = pd.DataFrame(np.random.randn(5, 2), columns=list("ab"))

In [19]: newcol = np.random.randn(len(df))

In [20]: df.eval("b + @newcol")
Out[20]: 
0   -0.206122
1   -1.029587
2    0.519726
3   -2.052589
4    1.453210
dtype: float64

In [21]: df.query("b < @newcol")
Out[21]: 
          a         b
1  0.160268 -0.848896
3  0.333758 -1.180355
4  0.572182  0.439895

If you don’t prefix the local variable with @, pandas will raise an exception telling you the variable is undefined.

When using DataFrame.eval() and DataFrame.query(), this allows you to have a local variable and a DataFrame column with the same name in an expression.

In [22]: a = np.random.randn()

In [23]: df.query("@a < a")
Out[23]: 
          a         b
0  0.473349  0.891236
1  0.160268 -0.848896
2  0.803311  1.662031
3  0.333758 -1.180355
4  0.572182  0.439895

In [24]: df.loc[a < df["a"]]  # same as the previous expression
Out[24]: 
          a         b
0  0.473349  0.891236
1  0.160268 -0.848896
2  0.803311  1.662031
3  0.333758 -1.180355
4  0.572182  0.439895

Warning

pandas.eval() will raise an exception if you cannot use the @ prefix because it isn’t defined in that context.

In [25]: a, b = 1, 2

In [26]: pd.eval("@a + b")
Traceback (most recent call last):

  File ~/micromamba/envs/test/lib/python3.10/site-packages/IPython/core/interactiveshell.py:3550 in run_code
    exec(code_obj, self.user_global_ns, self.user_ns)

  Cell In[26], line 1
    pd.eval("@a + b")

  File ~/work/pandas/pandas/pandas/core/computation/eval.py:325 in eval
    _check_for_locals(expr, level, parser)

  File ~/work/pandas/pandas/pandas/core/computation/eval.py:167 in _check_for_locals
    raise SyntaxError(msg)

  File <string>
SyntaxError: The '@' prefix is not allowed in top-level eval calls.
please refer to your variables by name without the '@' prefix.

In this case, you should simply refer to the variables like you would in standard Python.

In [27]: pd.eval("a + b")
Out[27]: 3

`pandas.eval()` parsers#

There are two different expression syntax parsers.

The default 'pandas' parser allows a more intuitive syntax for expressing query-like operations (comparisons, conjunctions and disjunctions). In particular, the precedence of the & and | operators is made equal to the precedence of the corresponding boolean operations and and or.

For example, the above conjunction can be written without parentheses. Alternatively, you can use the 'python' parser to enforce strict Python semantics.

In [28]: nrows, ncols = 20000, 100

In [29]: df1, df2, df3, df4 = [pd.DataFrame(np.random.randn(nrows, ncols)) for _ in range(4)]

In [30]: expr = "(df1 > 0) & (df2 > 0) & (df3 > 0) & (df4 > 0)"

In [31]: x = pd.eval(expr, parser="python")

In [32]: expr_no_parens = "df1 > 0 & df2 > 0 & df3 > 0 & df4 > 0"

In [33]: y = pd.eval(expr_no_parens, parser="pandas")

In [34]: np.all(x == y)
Out[34]: True

The same expression can be “anded” together with the word and as well:

In [35]: expr = "(df1 > 0) & (df2 > 0) & (df3 > 0) & (df4 > 0)"

In [36]: x = pd.eval(expr, parser="python")

In [37]: expr_with_ands = "df1 > 0 and df2 > 0 and df3 > 0 and df4 > 0"

In [38]: y = pd.eval(expr_with_ands, parser="pandas")

In [39]: np.all(x == y)
Out[39]: True

The and and or operators here have the same precedence that they would in Python.

`pandas.eval()` engines#

There are two different expression engines.

The 'numexpr' engine is the more performant engine that can yield performance improvements compared to standard Python syntax for large DataFrame. This engine requires the optional dependency numexpr to be installed.

The 'python' engine is generally not useful except for testing other evaluation engines against it. You will achieve no performance benefits using eval() with engine='python' and may incur a performance hit.

In [40]: %timeit df1 + df2 + df3 + df4
7.41 ms +- 41.2 us per loop (mean +- std. dev. of 7 runs, 100 loops each)

In [41]: %timeit pd.eval("df1 + df2 + df3 + df4", engine="python")
8.05 ms +- 46 us per loop (mean +- std. dev. of 7 runs, 100 loops each)

The `DataFrame.eval()` method#

In addition to the top level pandas.eval() function you can also evaluate an expression in the “context” of a DataFrame.

In [42]: df = pd.DataFrame(np.random.randn(5, 2), columns=["a", "b"])

In [43]: df.eval("a + b")
Out[43]: 
0   -0.161099
1    0.805452
2    0.747447
3    1.189042
4   -2.057490
dtype: float64

Any expression that is a valid pandas.eval() expression is also a valid DataFrame.eval() expression, with the added benefit that you don’t have to prefix the name of the DataFrame to the column(s) you’re interested in evaluating.

In addition, you can perform assignment of columns within an expression. This allows for formulaic evaluation. The assignment target can be a new column name or an existing column name, and it must be a valid Python identifier.

In [44]: df = pd.DataFrame(dict(a=range(5), b=range(5, 10)))

In [45]: df = df.eval("c = a + b")

In [46]: df = df.eval("d = a + b + c")

In [47]: df = df.eval("a = 1")

In [48]: df
Out[48]: 
   a  b   c   d
0  1  5   5  10
1  1  6   7  14
2  1  7   9  18
3  1  8  11  22
4  1  9  13  26

A copy of the DataFrame with the new or modified columns is returned, and the original frame is unchanged.

In [49]: df
Out[49]: 
   a  b   c   d
0  1  5   5  10
1  1  6   7  14
2  1  7   9  18
3  1  8  11  22
4  1  9  13  26

In [50]: df.eval("e = a - c")
Out[50]: 
   a  b   c   d   e
0  1  5   5  10  -4
1  1  6   7  14  -6
2  1  7   9  18  -8
3  1  8  11  22 -10
4  1  9  13  26 -12

In [51]: df
Out[51]: 
   a  b   c   d
0  1  5   5  10
1  1  6   7  14
2  1  7   9  18
3  1  8  11  22
4  1  9  13  26

Multiple column assignments can be performed by using a multi-line string.

In [52]: df.eval(
   ....:     """
   ....: c = a + b
   ....: d = a + b + c
   ....: a = 1""",
   ....: )
   ....: 
Out[52]: 
   a  b   c   d
0  1  5   6  12
1  1  6   7  14
2  1  7   8  16
3  1  8   9  18
4  1  9  10  20

The equivalent in standard Python would be

In [53]: df = pd.DataFrame(dict(a=range(5), b=range(5, 10)))

In [54]: df["c"] = df["a"] + df["b"]

In [55]: df["d"] = df["a"] + df["b"] + df["c"]

In [56]: df["a"] = 1

In [57]: df
Out[57]: 
   a  b   c   d
0  1  5   5  10
1  1  6   7  14
2  1  7   9  18
3  1  8  11  22
4  1  9  13  26

`eval()` performance comparison#

pandas.eval() works well with expressions containing large arrays.

In [58]: nrows, ncols = 20000, 100

In [59]: df1, df2, df3, df4 = [pd.DataFrame(np.random.randn(nrows, ncols)) for _ in range(4)]

DataFrame arithmetic:

In [60]: %timeit df1 + df2 + df3 + df4
7.41 ms +- 46.5 us per loop (mean +- std. dev. of 7 runs, 100 loops each)

In [61]: %timeit pd.eval("df1 + df2 + df3 + df4")
2.92 ms +- 38.7 us per loop (mean +- std. dev. of 7 runs, 100 loops each)

DataFrame comparison:

In [62]: %timeit (df1 > 0) & (df2 > 0) & (df3 > 0) & (df4 > 0)
6 ms +- 36.7 us per loop (mean +- std. dev. of 7 runs, 100 loops each)

In [63]: %timeit pd.eval("(df1 > 0) & (df2 > 0) & (df3 > 0) & (df4 > 0)")
9.42 ms +- 60.1 us per loop (mean +- std. dev. of 7 runs, 100 loops each)

DataFrame arithmetic with unaligned axes.

In [64]: s = pd.Series(np.random.randn(50))

In [65]: %timeit df1 + df2 + df3 + df4 + s
12.9 ms +- 127 us per loop (mean +- std. dev. of 7 runs, 100 loops each)

In [66]: %timeit pd.eval("df1 + df2 + df3 + df4 + s")
3.89 ms +- 55 us per loop (mean +- std. dev. of 7 runs, 100 loops each)

Note

Operations such as

1 and 2  # would parse to 1 & 2, but should evaluate to 2
3 or 4  # would parse to 3 | 4, but should evaluate to 3
~1  # this is okay, but slower when using eval

should be performed in Python. An exception will be raised if you try to perform any boolean/bitwise operations with scalar operands that are not of type bool or np.bool_.

Here is a plot showing the running time of pandas.eval() as function of the size of the frame involved in the computation. The two lines are two different engines.

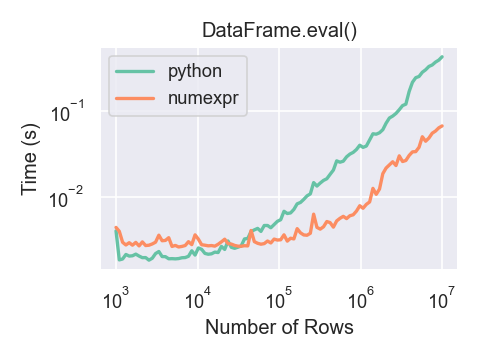
You will only see the performance benefits of using the numexpr engine with pandas.eval() if your DataFrame has more than approximately 100,000 rows.

This plot was created using a DataFrame with 3 columns each containing floating point values generated using numpy.random.randn().

Expression evaluation limitations with `numexpr`#

Expressions that would result in an object dtype or involve datetime operations because of NaT must be evaluated in Python space, but part of an expression can still be evaluated with numexpr. For example:

In [67]: df = pd.DataFrame(
   ....:     {"strings": np.repeat(list("cba"), 3), "nums": np.repeat(range(3), 3)}
   ....: )
   ....: 

In [68]: df
Out[68]: 
  strings  nums
0       c     0
1       c     0
2       c     0
3       b     1
4       b     1
5       b     1
6       a     2
7       a     2
8       a     2

In [69]: df.query("strings == 'a' and nums == 1")
Out[69]: 
Empty DataFrame
Columns: [strings, nums]
Index: []

The numeric part of the comparison (nums == 1) will be evaluated by numexpr and the object part of the comparison ("strings == 'a') will be evaluated by Python.

Enhancing performance#

Cython (writing C extensions for pandas)#

Pure Python#

Plain Cython#

Declaring C types#

Using ndarray#

Disabling compiler directives#

Numba (JIT compilation)#

pandas Numba Engine#

Custom Function Examples#

Caveats#

Expression evaluation via eval()#

Supported syntax#

Local variables#

pandas.eval() parsers#

pandas.eval() engines#

The DataFrame.eval() method#

eval() performance comparison#

Expression evaluation limitations with numexpr#

Expression evaluation via `eval()`#

`pandas.eval()` parsers#

`pandas.eval()` engines#

The `DataFrame.eval()` method#

`eval()` performance comparison#

Expression evaluation limitations with `numexpr`#